Union/Intersection Description and Calculation
What is Union
If A and B are sets, then the union of A and B |A∪B | is a set with all elements of A and all elements of B, but no other elements.
It is more commonly used in probability analysis, such as: if the probability of event A is 0.3 and the probability of event B is 0.2, what is the probability of event A or B?
If event A or event B occurs, it is |A∪B |.
What is intersection
The intersection of A and B is a set that contains all the elements that belong to both A and B, but no other elements.
In terms of probability, if the probability of event A is 0.3 and the probability of event B is 0.2, then what is the probability of event A and event B?
If an event A occurs and an event B occurs, it is | A∩B |. The calculation is the probability of occurrence of A event multiplied by the probability of occurrence of B event, which is 0.3*0.2=0.06.
2 Unions Calculation Instructions
The following figure shows that the occurrence of A or B is equivalent to “A plus B minus the overlap between A and B.”
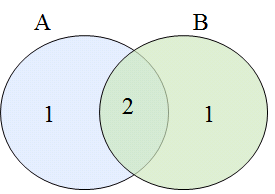
As shown in the figure above, if A is added to B, there will be one more overlap in the middle, so it needs to be deducted.
|A∪B | = |A |+ |B |- | A∩B |
If the probability of event A is 0.3 and the probability of event B is 0.2, what is the probability of event A or event B?
|A∪B |=0.3+0.2-0.3*0.2=0.44
3 Unions Calculation Instructions
As shown in the figure above, if there are two overlaps of A plus B plus C, there will also be three overlaps.
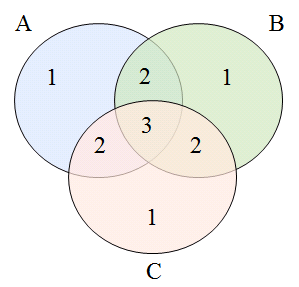
First, you need to deduct the two overlapping places first, |A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|, after deduction, it will become the following figure.
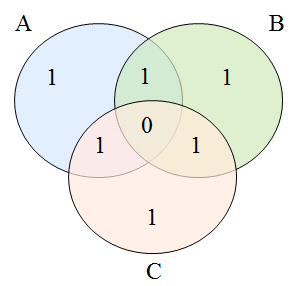
After deducting the overlapping place twice, there is one remaining, but the place overlapping three times is deducted, so it needs to be added back, and the part overlapping A, B, C in the middle is |A∩B∩C|, combined together As follows:
|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|
If the probability of event A is 0.3, the probability of event B is 0.2, and the probability of event C is 0.1, what is the probability of event A or event B or event C?
|A∪B∪C|=(0.3)+(0.2)+(0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.3*0.2*0.1)=0.6-0.06-0.03-0.02+0.006=0.496
Inclusion-Exclusion Principle
According to the formula of the 2 unions and the 3 unions, we can find a regularity.
|A∪B | = |A |+ |B |- | A∩B | (single – double)
|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C (single – double + three)
Have you noticed the rule of “positive” first, then “negative”, and then “positive”; the same is true for the part of the collection, first “single”, then “double”, then “three”, yes, This is the Inclusion-Exclusion Principle.
What about the 4 unions? That is, single – double + three – four.
The mathematical formula of the Inclusion-Exclusion Principle is
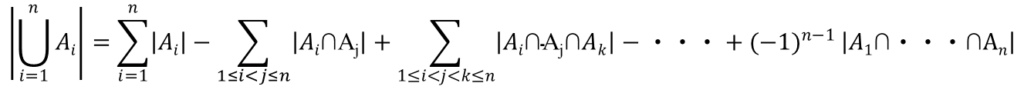
4 Unions Calculation Instructions
The 4 unions are single – double + three – four.
|A∪B ∪C ∪D | = |A |+ |B |+ |C |+|D | – | A∩B |-| A∩C |-| A∩D |-| B∩C |-| B∩D |-| C∩D |+ | A∩B∩C |+| A∩B∩D |+| A∩C∩D |+ | B∩C∩D | – | A ∩ B∩C∩D |
If the probability of event A is 0.4, the probability of event B is 0.3, the probability of event C is 0.2, and the probability of event D is 0.1, what is the probability of event A or B or C or D? ?
|A∪B ∪C ∪D |=(0.4)+(0.3)+(0.2)+(0.1)-(0.4*0.3)-(0.4*0.2)-(0.4*0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.4*0.3*0.2)+(0.4*0.3*0.1)+(0.4*0.2*0.1)+(0.3*0.2*0.1)-(0.4*0.3*0.2*0.1)=1-0.12-0.08-0.04-0.06-0.03-0.02+0.024+0.012+0.008+0.006-0.0024=0.6976
5 Unions Calculation Instructions
The 5 unions are single – double + three – four + five.
|A∪B∪C∪D∪E|=|A|+|B|+|C|+|D|+|E|-|A∩B|-|A∩C|-|A∩D|-|A∩E|-|B∩C|-|B∩D|-|B∩E|-|C∩D|-|C∩E|-|D∩E|+|A∩B∩C|+|A∩B∩D|+|A∩B∩E|+|A∩C∩D|+|A∩C∩E|+|A∩D∩E|+|B∩C∩D|+|B∩C∩E|+|B∩D∩E|+|C∩D∩E|-|A∩B∩C∩D|-|A∩B∩C∩E| -|A∩B∩D∩E|-|A∩C∩D∩E|-|B∩C∩D∩E|+|A∩B∩C∩D∩E|
If the probability of event A is 0.5, the probability of event B is 0.4, the probability of event C is 0.3, the probability of event D is 0.2, and the probability of event E is 0.1, then event A or event B or event C occurs Or what is the probability of event D or event E?
|A∪B∪C∪D∪E|=(0.5)+(0.4)+(0.3)+(0.2)+(0.1)-(0.5*0.4)-(0.5*0.3)-(0.5*0.2)-(0.5*0.1)-(0.4*0.3)-(0.4*0.2)-(0.4*0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.5*0.4*0.3)+(0.5*0.4*0.2)+(0.5*0.4*0.1)+(0.5*0.3*0.2)+(0.5*0.3*0.1)+(0.5*0.2*0.1)+(0.4*0.3*0.2)+(0.4*0.3*0.1)+(0.4*0.2*0.1)+(0.3*0.2*0.1)-(0.5*0.4*0.3*0.2)-(0.5*0.4*0.3*0.1)-(0.5*0.4*0.2*0.1)-(0.5*0.3*0.2*0.1)-(0.4*0.3*0.2*0.1)+(0.5*0.4*0.3*0.2*0.1)=0.8488
2 Unions/3 Unions/4 Unions/5 Unions Calculator
Please link to the following for union calculation.