【輸入數值自動計算聯集】三項聯集/四項聯集/五項聯集計算(排容原理)

內容目錄

聯集/交集說明與計算

輸入數值計算聯集

為了幫大家快速計算，以下根據兩項、三項、四項、五項輸入數值計算出聯集，若想深入了解請再往下看。

什麼是聯集

若A與B是集合，則A與B的聯集｜A∪B ｜是有所有A的元素和所有B的元素，而沒有其他元素的集合。
較常用在機率分析裡，像：如果A事件發生的機率為0.3，B事件發生的機率為0.2，那發生A事件或B事件的機率為何呢？
發生A事件或B事件則為｜A∪B ｜。

什麼是交集

A和B的交集是含有所有既屬於A又屬於B的元素，而沒有其他元素的集合。
同樣以機率來說明，如果A事件發生的機率為0.3，B事件發生的機率為0.2，那發生A事件又發生B事件的機率為何呢？
發生A事件又發生B事件則為｜ A∩B ｜，計算則為A事件發生的機率乘上B事件發生的機率，也就是0.3*0.2=0.06。

兩項聯集計算說明

兩項聯集是相對簡單及普遍的，以下方圖示說明，發生A或是發生B也就等於「A加上B在扣除A和B重疊的部份。」

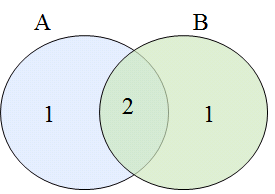
可以看到上方圖，如果A加上B的話，中間重疊的地方會多了一次，所以需要扣除。

｜A∪B ｜ = ｜A ｜+ ｜B ｜- ｜ A∩B ｜

如果A事件發生的機率為0.3，B事件發生的機率為0.2，那發生A事件或B事件的機率為何呢？

｜A∪B ｜=0.3+0.2-0.3*0.2=0.44

三項聯集計算說明

如果A事件發生的機率為0.3，B事件發生的機率為0.2，C事件發生的機率為0.1，那發生A事件或B事件或C事件的機率為何呢？
以下面圖示來說明，雖然相較於兩項聯集稍微複雜一點，但不難理解。

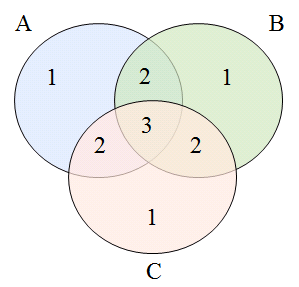
如上圖，若A加B加C會出現重疊兩次的地方，也涵蓋到三次重疊的地方。
首先需要先扣除兩次重疊的地方，｜A｜+｜B｜+｜C｜-｜A∩B｜-｜A∩C｜-｜B∩C｜，扣除後會變成以下圖形。

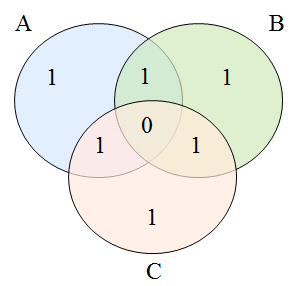
會發現兩次的地方扣除後，剩餘一次，但重疊三次的地方也被扣光了，所以需要再加回去，而中間重疊A、B、C的部分即為｜A∩B∩C｜，合起來則為如下：

｜A∪B∪C｜=｜A｜+｜B｜+｜C｜-｜A∩B｜-｜A∩C｜-｜B∩C｜+｜A∩B∩C｜

｜A∪B∪C｜=(0.3)+(0.2)+(0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.3*0.2*0.1)=0.6-0.06-0.03-0.02+0.006=0.496

排容原理

依照兩項聯集、三項聯集的公式，有沒有發現可以找到個規律性。

｜A∪B ｜ = ｜A ｜+ ｜B ｜- ｜ A∩B ｜ (單個集合-雙個集合)
｜A∪B∪C｜=｜A｜+｜B｜+｜C｜-｜A∩B｜-｜A∩C｜-｜B∩C｜+｜A∩B∩C｜ (單個集合-雙個集合+三個集合)
有沒有發現先是「正」，再來是「負」，接著是「正」的規律；集合的部分也是，先是「單個集合」，再來是「雙個集合」，接著是「三個集合」，沒錯，這就是排容原理。
那四個集合聯集呢？也就是單個集合-雙個集合+三個集合-四個集合。

排容原理寫成數學式為：

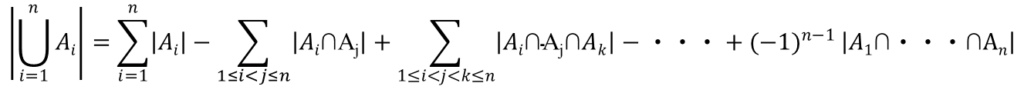
以前數學忘的差不多了嗎，沒關係，你只要記得正負正負就好。

四項聯集計算說明

四項聯集是立體的概念，A與B與C與D交會，有四項重疊的地方｜A∩B∩C∩D｜，但又有三項重疊但不與第四項重疊的地方｜A∩B∩C｜、｜A∩B∩D｜、｜A∩C∩D｜、｜B∩C∩D｜。
是不是覺得四項聯集不好以圖形來想像呢？那麼該怎麼計算四項聯集呢？
如果A事件發生的機率為0.4，B事件發生的機率為0.3，C事件發生的機率為0.2，D事件發生的機率為0.1，那發生A事件或B事件或C事件或D事件的機率為何呢？
也就是｜A∪B ∪C ∪D ｜，會覺得數學式我也會寫，那怎麼展開呢？
就要用剛剛提到的排容公式來計算啦！

四項聯集也就是：單個集合-雙個集合+三個集合-四個集合

｜A∪B ∪C ∪D ｜ = ｜A ｜+ ｜B ｜+ ｜C ｜+｜D ｜ – ｜ A∩B ｜-｜ A∩C ｜-｜ A∩D ｜-｜ B∩C ｜-｜ B∩D ｜-｜ C∩D ｜+ ｜ A∩B∩C ｜+｜ A∩B∩D ｜+｜ A∩C∩D ｜+ ｜ B∩C∩D ｜ – ｜ A ∩ B∩C∩D ｜

｜A∪B ∪C ∪D ｜=(0.4)+(0.3)+(0.2)+(0.1)-(0.4*0.3)-(0.4*0.2)-(0.4*0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.4*0.3*0.2)+(0.4*0.3*0.1)+(0.4*0.2*0.1)+(0.3*0.2*0.1)-(0.4*0.3*0.2*0.1)=1-0.12-0.08-0.04-0.06-0.03-0.02+0.024+0.012+0.008+0.006-0.0024=0.6976

五項聯集計算說明

遇到五項聯集怎麼計算呢？沒錯，排容原理，正負正負正。
如果A事件發生的機率為0.5，B事件發生的機率為0.4，C事件發生的機率為0.3，D事件發生的機率為0.2，E發生的機率為0.1，那發生A事件或B事件或C事件或D事件或E事件的機率為何呢？

｜A∪B∪C∪D∪E｜=｜A｜+｜B｜+｜C｜+｜D｜+｜E｜-｜A∩B｜-｜A∩C｜-｜A∩D｜-｜A∩E｜-｜B∩C｜-｜B∩D｜-｜B∩E｜-｜C∩D｜-｜C∩E｜-｜D∩E｜+｜A∩B∩C｜+｜A∩B∩D｜+｜A∩B∩E｜+｜A∩C∩D｜+｜A∩C∩E｜+｜A∩D∩E｜+｜B∩C∩D｜+｜B∩C∩E｜+｜B∩D∩E｜+｜C∩D∩E｜-｜A∩B∩C∩D｜-｜A∩B∩C∩E｜ -｜A∩B∩D∩E｜-｜A∩C∩D∩E｜-｜B∩C∩D∩E｜+｜A∩B∩C∩D∩E｜

｜A∪B∪C∪D∪E｜=(0.5)+(0.4)+(0.3)+(0.2)+(0.1)-(0.5*0.4)-(0.5*0.3)-(0.5*0.2)-(0.5*0.1)-(0.4*0.3)-(0.4*0.2)-(0.4*0.1)-(0.3*0.2)-(0.3*0.1)-(0.2*0.1)+(0.5*0.4*0.3)+(0.5*0.4*0.2)+(0.5*0.4*0.1)+(0.5*0.3*0.2)+(0.5*0.3*0.1)+(0.5*0.2*0.1)+(0.4*0.3*0.2)+(0.4*0.3*0.1)+(0.4*0.2*0.1)+(0.3*0.2*0.1)-(0.5*0.4*0.3*0.2)-(0.5*0.4*0.3*0.1)-(0.5*0.4*0.2*0.1)-(0.5*0.3*0.2*0.1)-(0.4*0.3*0.2*0.1)+(0.5*0.4*0.3*0.2*0.1)=0.8488