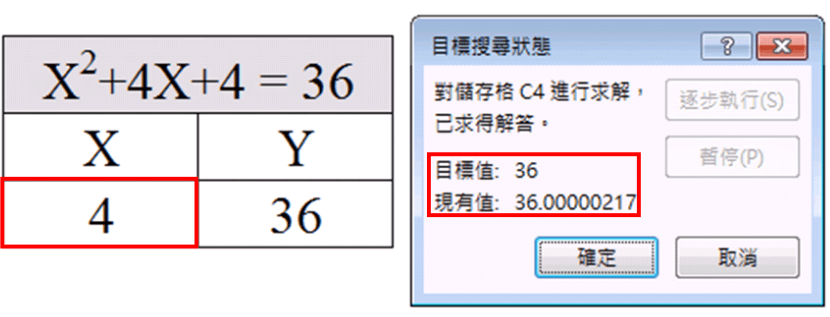
Excel解三元一次方程式

利用Excel來求解三元一次方程式,首先需要了解「矩陣概念」及兩個矩陣函數-「MINVERSE」與「MMULT」函數。
矩陣概念
不知道大家還記不記得「矩陣」、「反矩陣」?
如果你對於「矩陣」沒興趣的話,可以直接跳到下一段「Step1 列出係數及值」,反正會使用函數解出方程式就好。
如果你有興趣但忘記矩陣的話,那你可能需要翻下數學課本回憶一下。
矩陣&反矩陣
以下以2階矩陣為例子:
A、B∈Mnxn,若AB=I
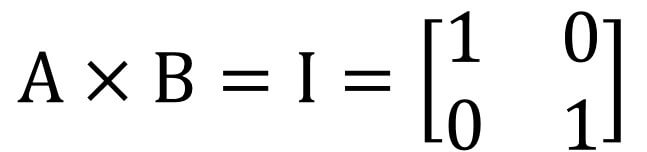
則A與B互為反矩陣,也可將B寫為A-1或將A寫為B-1。
B=A-1;A=B-1
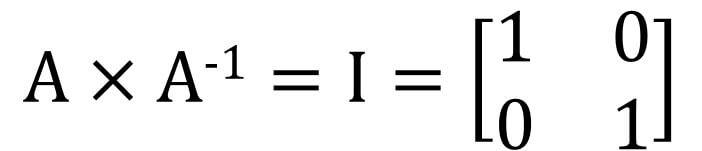
範例-矩陣
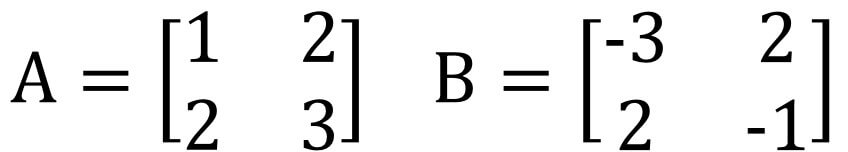
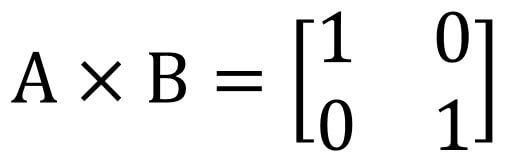
則A與B互為反矩陣。
矩陣運算
有一等式:A‧X=C,於左右兩邊各乘上A-1。
A-1‧AX=A-1‧C
X=A-1‧C
範例-矩陣運算
以下線性系統
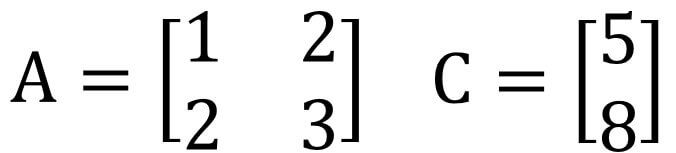
A的反矩陣A-1為以下
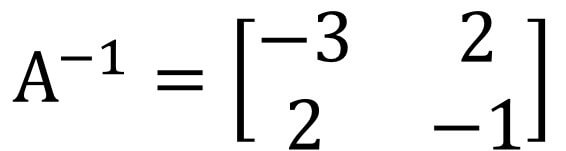
A‧X=C
A-1‧AX=A-1‧C
X=A-1‧C
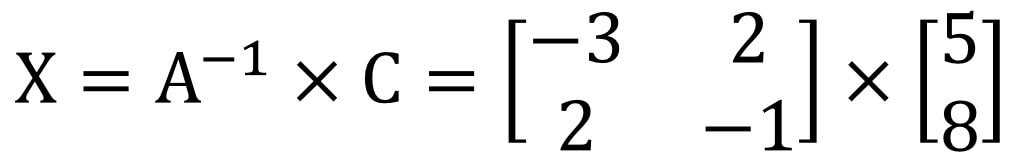
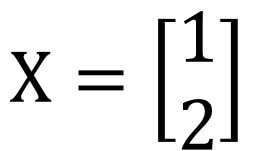
你可能會想~這樣的計算要做什麼用?
沒關係,換成以下表示你就清楚了。
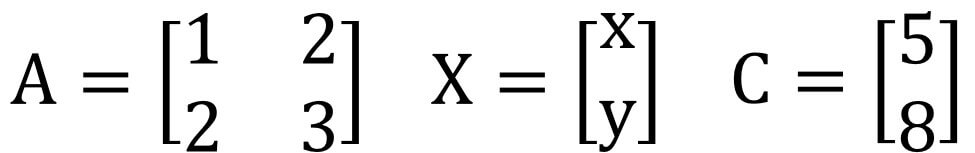
A‧X=C也就是以下的式子
1x+2y=5
2x+3y=8
求得X也就是解二元一次方程式
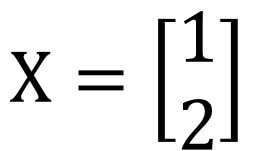
也就是x=1;y=2
所以接下來就是利用Excel的矩陣函數運算來解三元一次方程式。
Step1 列出係數及值
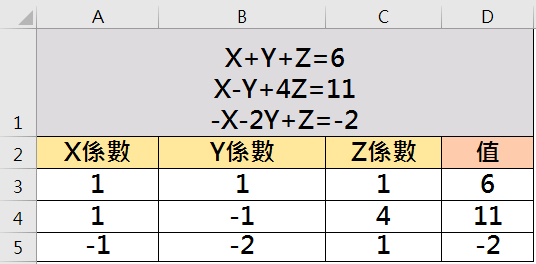
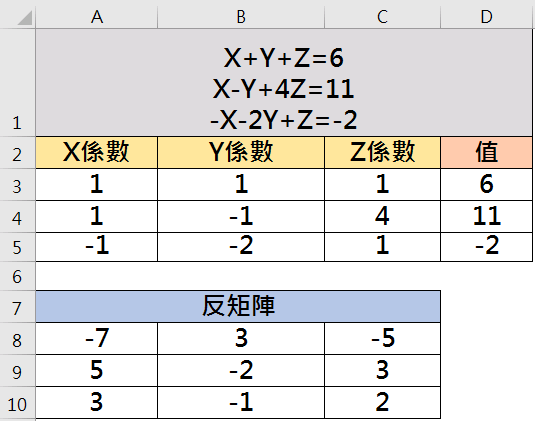
如解三元一次聯立方程式X+Y+X=6;X-Y+4Z=11;-X-2Y+Z=-2。
首先列出X、Y、Z係數及值如下所示
Step2 求出反矩陣
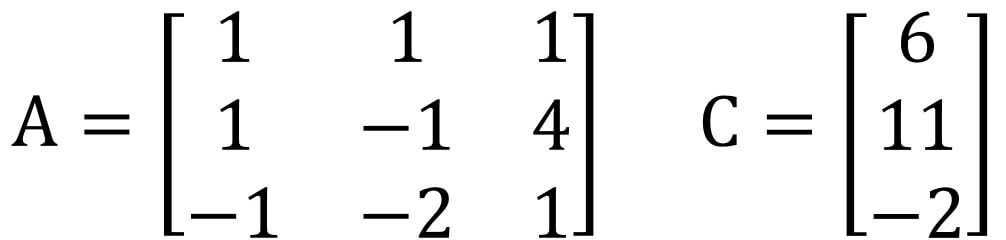
A為3列3行的矩陣,所以反矩陣也為3列3行。
框選3列3行的儲存格如「A8:C10」,點選插入函數f(x)-「MINVERSE」函數。
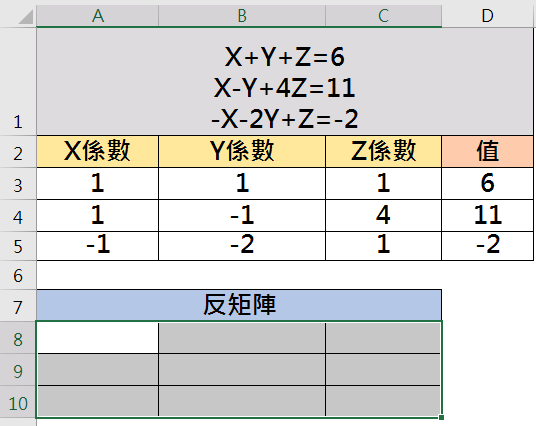
MINVERSE函數
傳回儲存於某陣列中之矩陣的反矩陣。
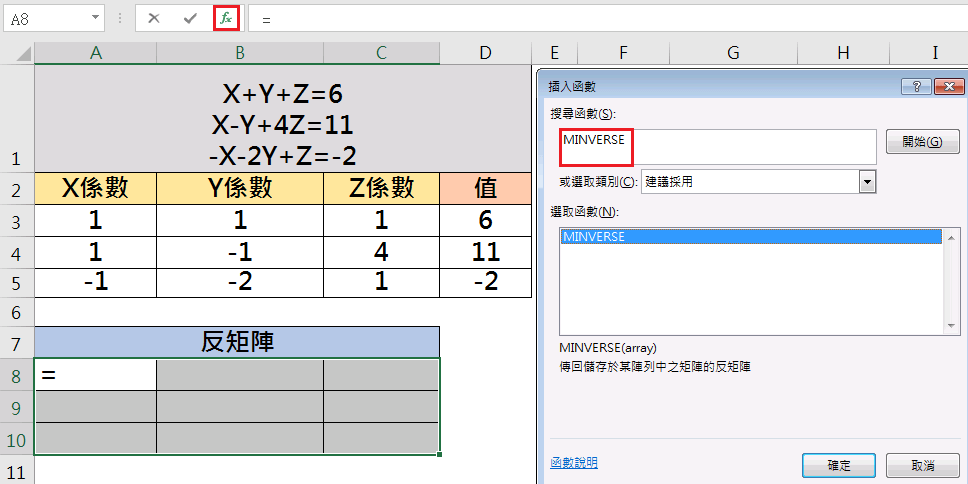
函數引數
Array:相同行數與列數的數值陣列,即A矩陣「A3:C5」儲存格。
※因矩陣需以陣列表示,我們需要按下「Ctrl」+「Shift」+「Enter」,轉為陣列表示。
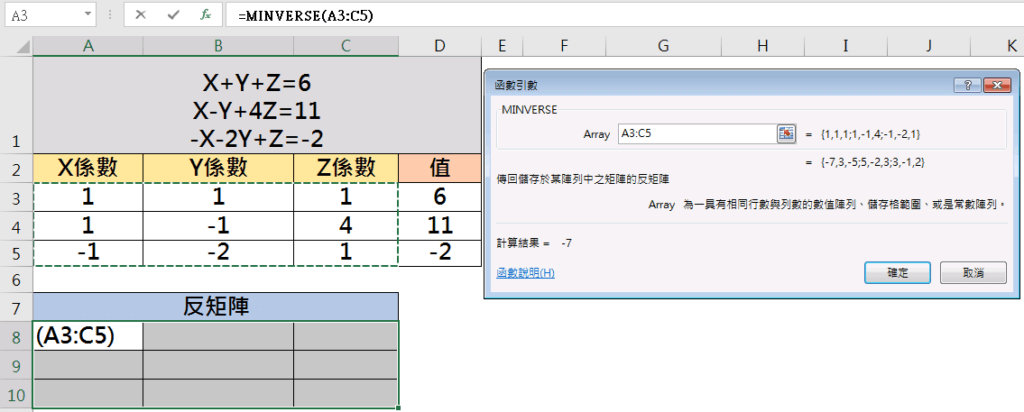
「Ctrl」+「Shift」+「Enter」後即求得矩陣A的反矩陣A-1。
Step3 反矩陣乘積
前面介紹二階矩陣提到以下
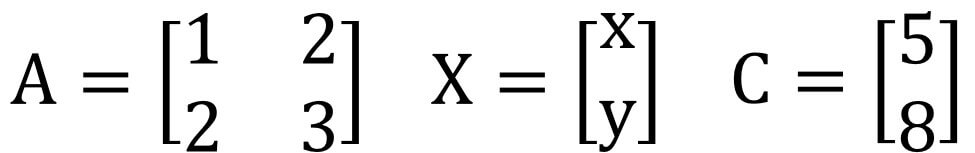
A‧X=C
A-1‧AX=A-1‧C
X=A-1‧C
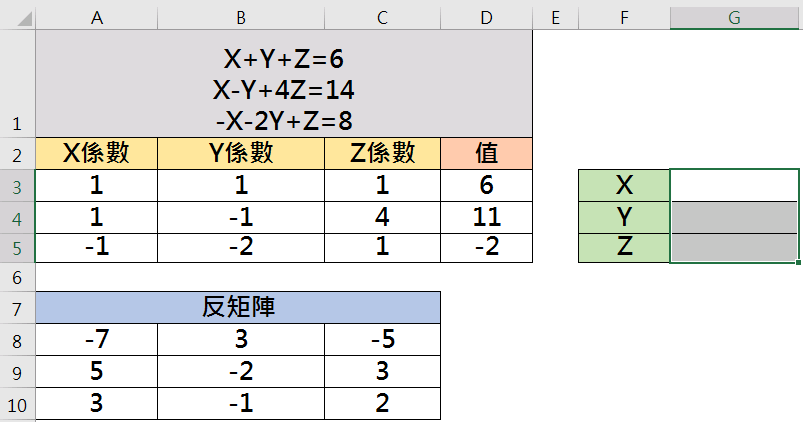
同樣的,三階矩陣只要利用求出的反矩陣A-1 X C,即可求得X、Y及Z值。
因X、Y及Z為三列一行矩陣,選取三列一行之儲存格如「G3:G4」,點選插入函數f(x)-「MMULT」函數。
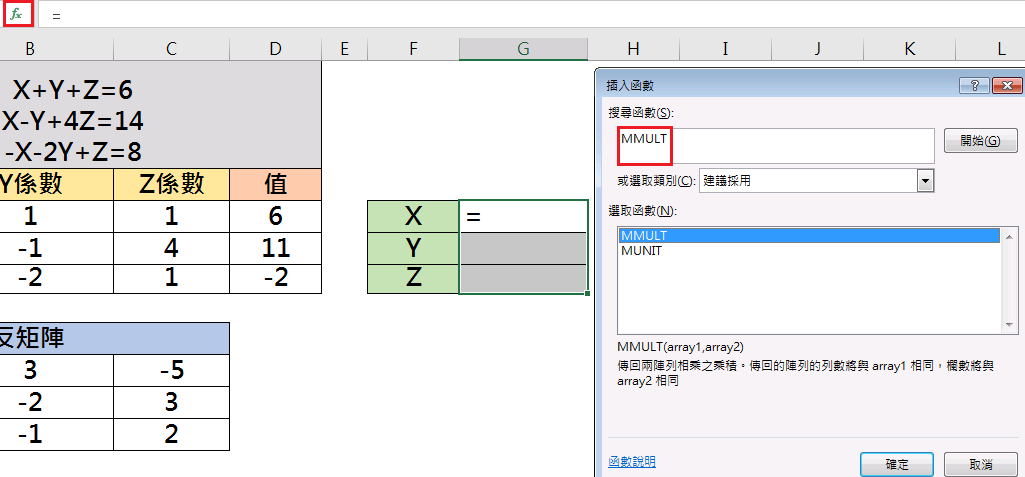
MMULT函數
傳回兩陣列相乘之乘積。
函數引數
X=A-1‧C
Array1:要相乘的第一個陣列,即為反矩陣A-1「A8:C10」儲存格。
Array2:要相乘的第二個陣列,即為C值「D3:D5」儲存格。
PS:順序不可顛倒,否則會錯誤。
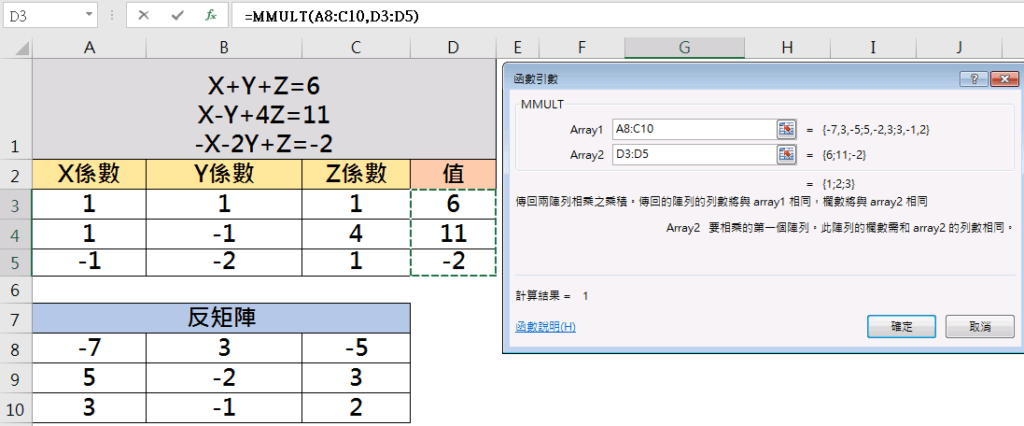
按下確定後會發現僅有一個值。
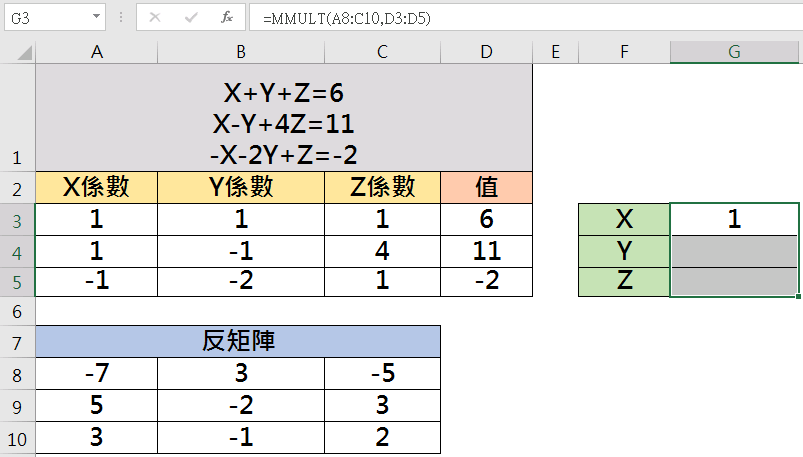
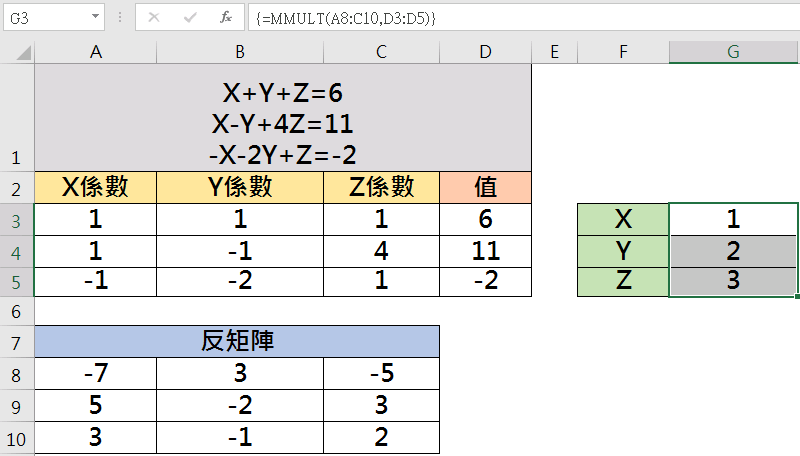
同前面一樣要以陣列表示,按下「Ctrl」+「Shift」+「Enter」即求得X及Y值。
則完成以Excel解三元一次方程式。
複合函數
如果你已經熟悉「MINVERSE」與「MMULT」函數,你可以直接將他們結合成複合函數,則不需要先算出反函數,再進行乘積。
Array1:計算「A3:B5」的反函數,即「Minverse(A3:C5)」。
Array2:選取C值,即「D3:D5」。
同樣的轉為陣列表示,按下「Ctrl」+「Shift」+「Enter」。

即一次求出X、Y及Z值。

Excel解二元一次方程式
點選以下連結了解「EXCEL解二元一次方程式」。