你知道Excel可以求解未知數嗎?
Excel求解方程的功能你知道嗎?
只要簡單幾步驟。
一元一次方程式
雖然一元一次方程式太簡單,但還是先用簡單的例子來說明,若9X=243,求X?
方法一、除法
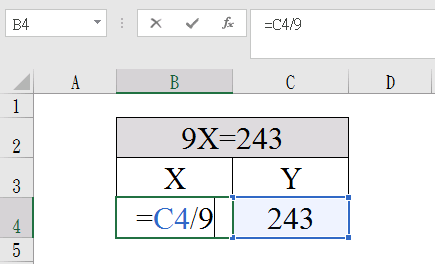
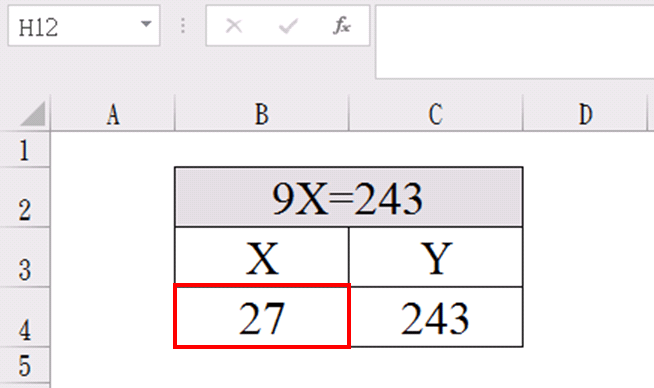
以一個儲存格為X值;一個儲存格為Y值,C4 (Y值)輸入「243」,B4 (X值)輸入「=C4/9」,或者直接儲存格寫上「=243/9」,按下Enter就求解了,X=27。
方法二、模擬分析
除法大家應該都會,但模擬分析可能就沒聽過了,也是Excel很有用的工具之一。
(1)寫上方程式
B4寫上「1」;C4寫上「=B4*9」,也就是當X=1時,Y等於多少的概念。
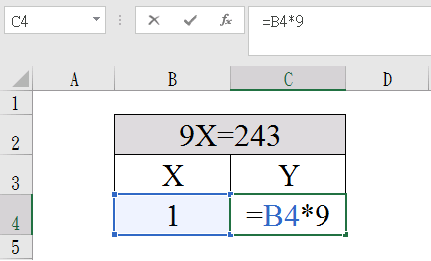
(2)開啟模擬分析
點選 資料-模擬分析-目標搜尋
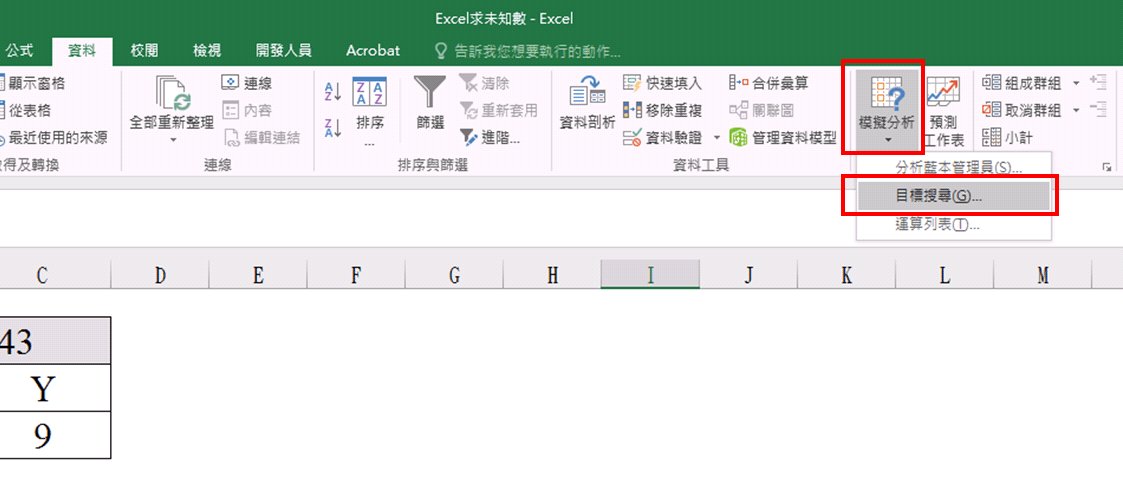
(3)設定目標搜尋
目標儲存格:點選C4 (剛設定的Y值也就是「=B4*9」)
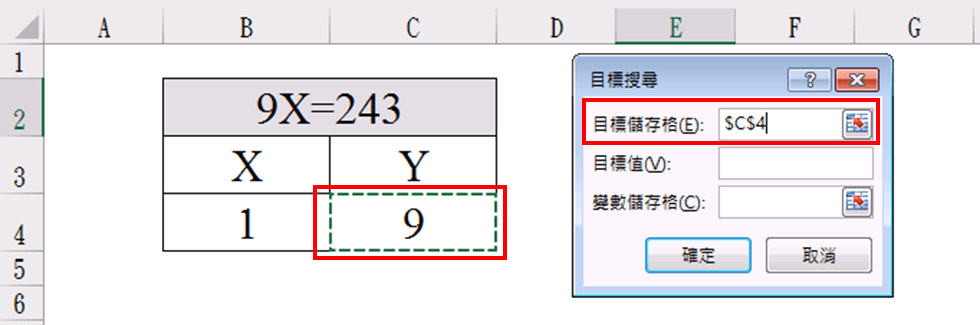
目標值:打上「243」(也就是要當Y=「243」(目標值)時,X要為多少?)
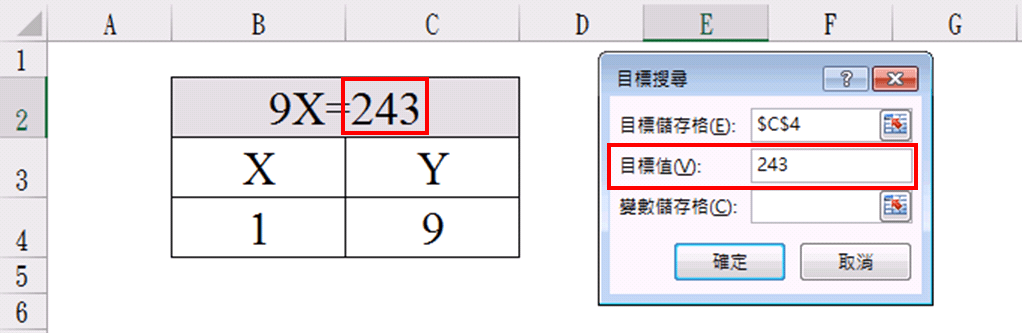
變數儲存格:點選B4 (也就是未知數x)
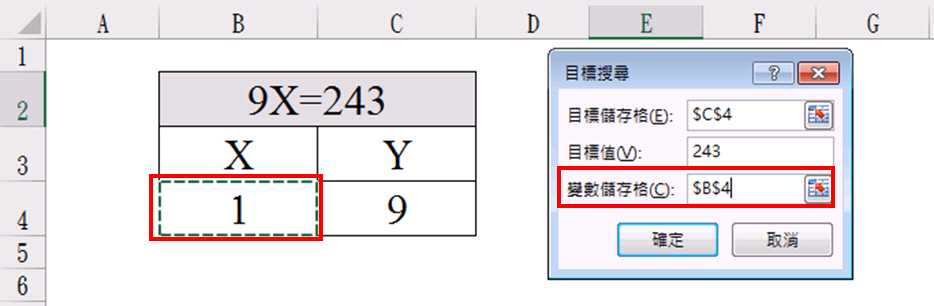
(4)點選「確定」
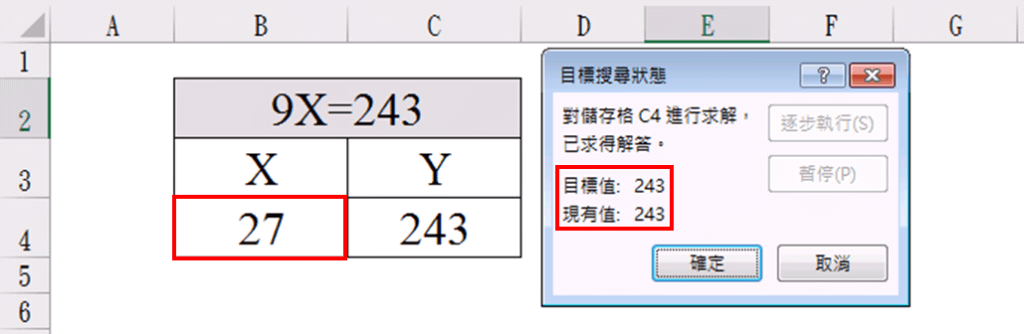
點選確定後,B4 (X值)即開始變動,由1開始一直往上增加,直到C4(Y值)達到目標值243時,X則停止,顯示27。
一元二次方程式
若X^2+4X+4 = 36,求X?
方法一、公式解
還有印象的話,應該對以下公式很熟悉。
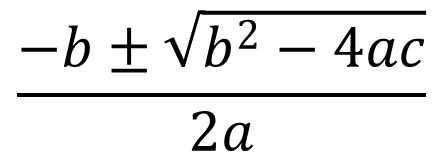
當b^2-4ac>0,則有兩個不同的實數根;當b^2-4ac=0,則有兩個相等的實數根;當b^2-4ac<0,則有有兩個不同的複數根,當b^2-4ac<0常被稱「無解」。
Excel也可以利用公式解法。
(1)改寫方程式
要使用公式解,首先要改成制式的方程式寫法→ ax^2+bx+c=0。
所以X^2+4X+4 = 36,就變成以下
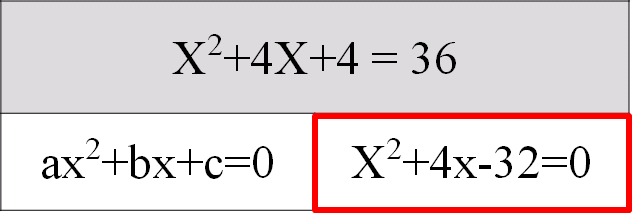
(2)取得a、b、c
改寫方程式後為X^2+4x-32
a=1、b=4、c=-32 。
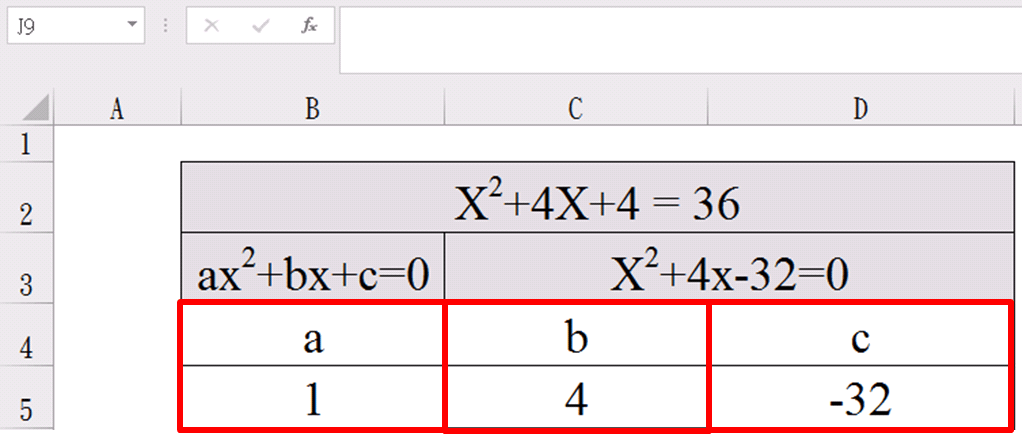
(3)建立公式解
公式解則會以兩個根/解如下
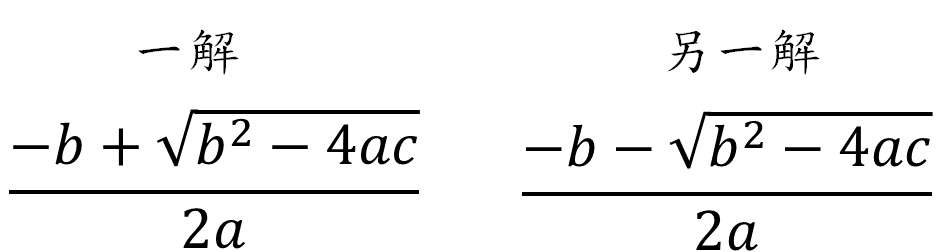
所以,一儲存格代入「=((-C5+(C5^2-4B5D5)^(1/2))/(2*B5))」,另一儲存格代入「=((-C5-(C5^2-4B5D5)^(1/2))/(2*B5))」,按下Enter後,即求得兩解。
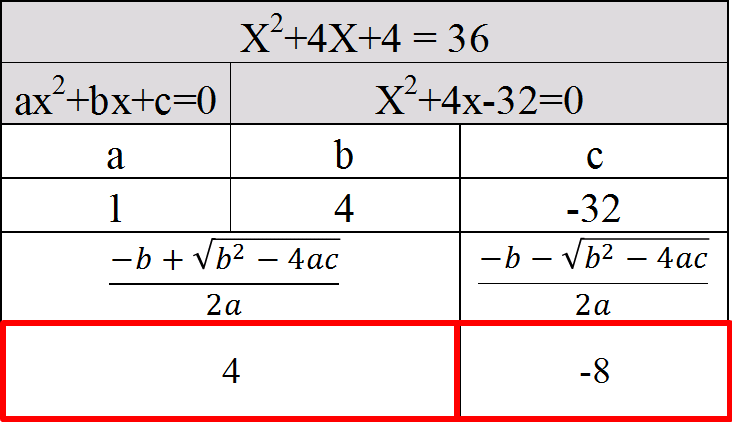
X= 4 or -8。
優點:建立好公式解,後續針對一元二次方程式,只需要輸入好a、b、c值,即可求得二解。
缺點:僅能針對一元二次方程式求解,且需要改成制式方程式寫法ax^2+bx+c=0,無法求得像是以下的未知數,但利用方法二模擬分析可以求得。
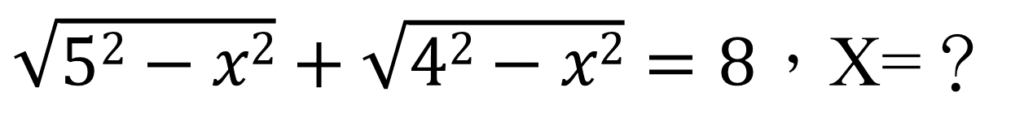
方法二、模擬分析
(1)寫上方程式
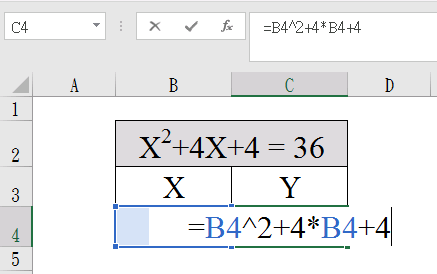
B4寫上「1」;C4寫上「=B4^2+4*B4+4」,也就是當X=1時,Y等於多少的概念。
(2)開啟模擬分析
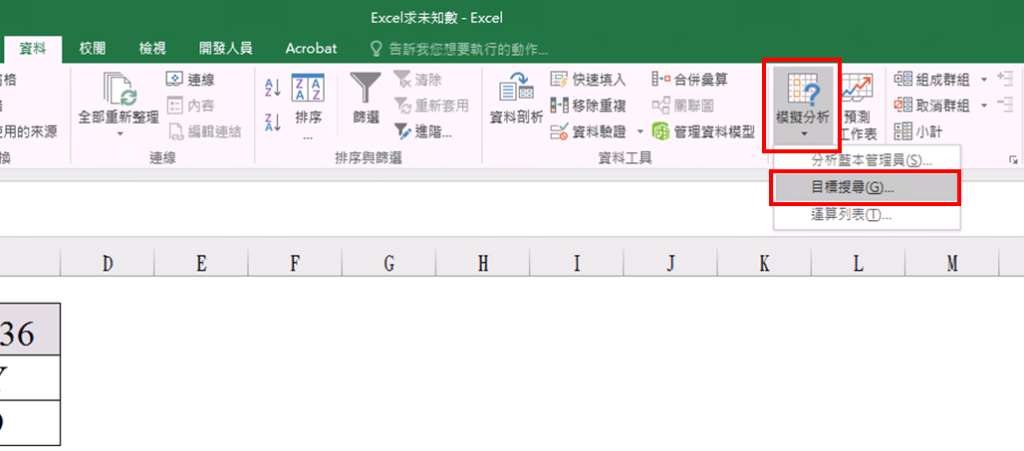
點選 資料-模擬分析-目標搜尋
(3)設定目標搜尋
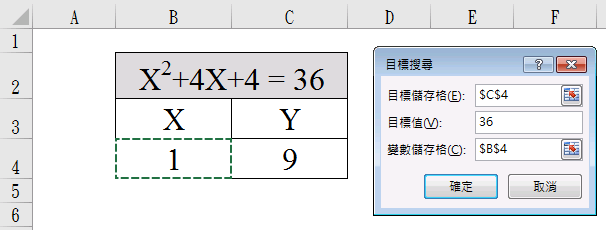
目標儲存格:點選C4 (剛設定的Y值也就是「=B4^2+4*B4+4」)
目標值:打上「36」(也就是要當Y=「36」(目標值)時,X要為多少?)
變數儲存格:點選B4 (也就是未知數x)
(4)點選「確定」得一解
點選確定後,B4 (X值)即開始變動,由1開始一直往上增加,直到C4(Y值)達到目標值36時,X則停止,顯示4。
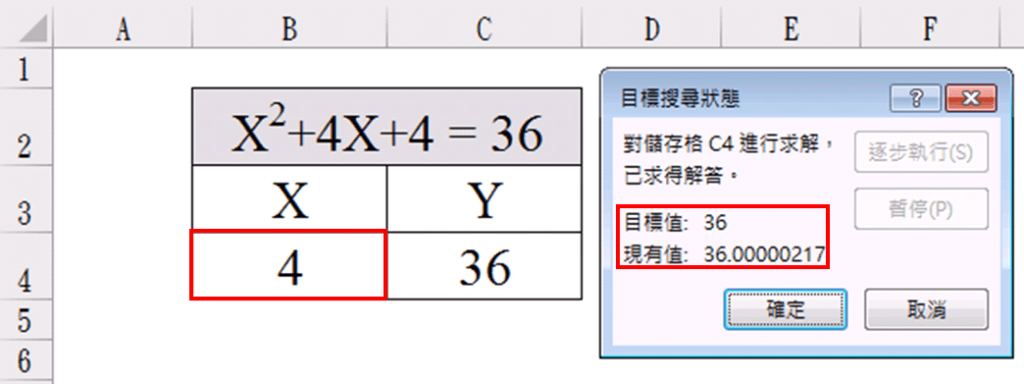
缺點:由於模擬分析是由小往大加,直到達到目標值,所以此方法只會求得一個解。
那要怎麼求第二個解呢?請往下看……
(5)求第二個解
如上所述,模擬分析是由小往大加,所以如果要找到更小的解,像是負數根/解,起始值就要輸入更小的值,如輸入-99或-999。
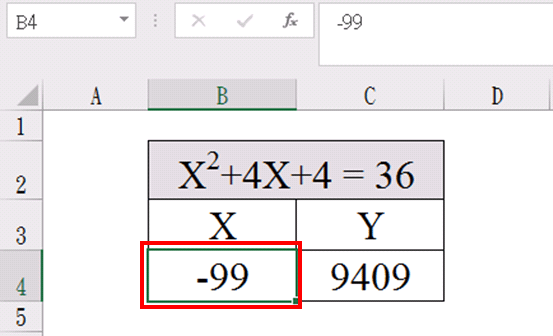
如前面同樣步驟,點選 資料-模擬分析-目標搜尋,設定目標搜尋
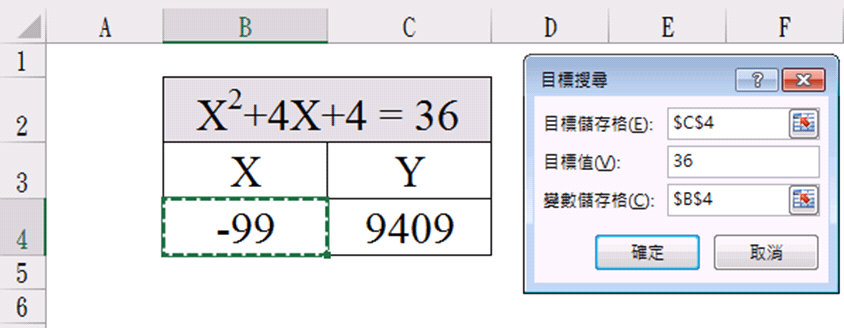
點選「確定」得另外一解。
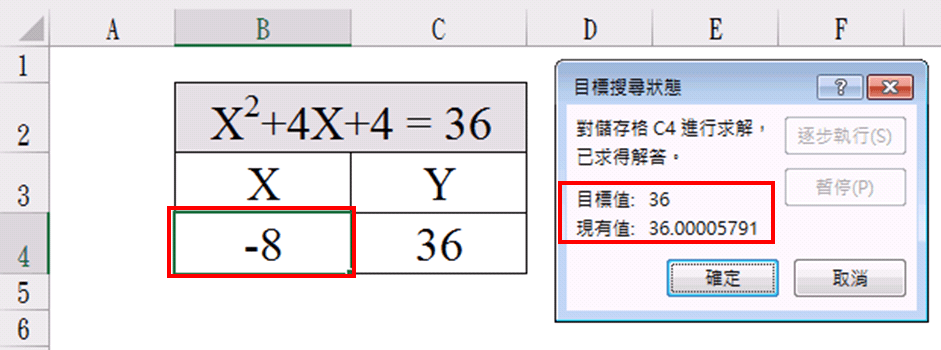
優點:模擬分析除了可以求一元一次方程式、一元二次方程式,甚至是一元三次方程式、一元多次方程式都可以求得。
只要設定好Excel公式函數,簡單幾步驟就能夠求出未知數。
不論在職場上或是生活中,「模擬分析-推測數值」絕對是很實用的工具。