兩個相同半徑的圓重疊面積計算可以參閱此篇。
那~兩不同半徑的圓重疊面積該如何計算呢？
其實也是相同的概念，差異只在於扇形面積的θ以及菱形面積的h，計算稍微複雜一點而已。
重疊面積計算教學
一個半徑為5cm的圓形與一個半徑為4cm的圓心相交，當兩個圓心距離8cm時，請問兩個圓所相交的重疊面積是多少呢？
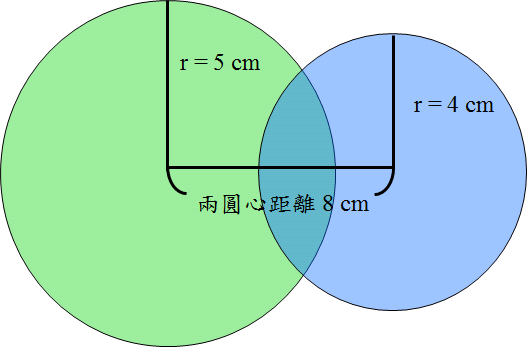
同樣的，前面的計算方式與計算兩個相同半徑的圓重疊面積相同，為四個扇形面積相加再扣除菱形面積。
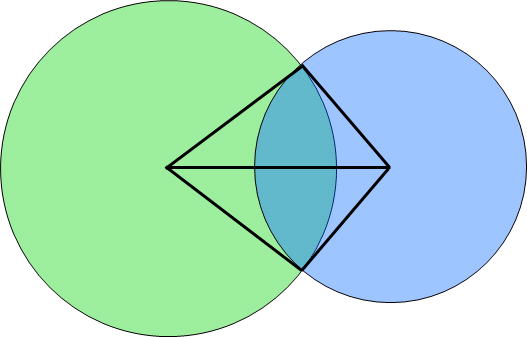
差異在「兩個相同半徑的圓是以四個相同扇形」做計算，而「兩個不同半徑的圓是兩個大的扇形加上兩個小的扇形」做計算。
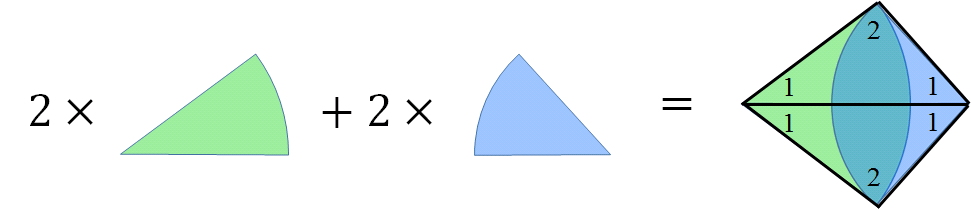
最困難的地方來了，要怎麼計算出θ1、θ2以及h呢？
我們先將已知數值標上。
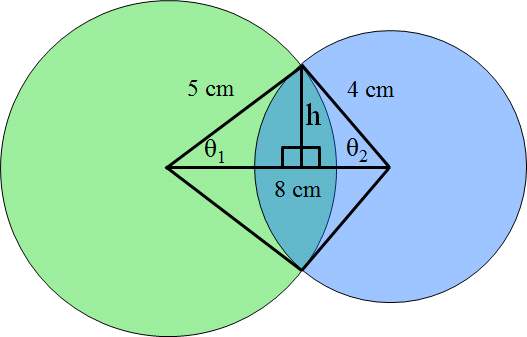
我們可以將大的三角形(5-4-8 cm)拆解成以下，並利用畢式定理(兩條直角邊長度分別是a和b，斜邊長度是c，則a^2+b^2=c^2，a=(c^2-b^2)^1/2。
所以，一邊三角形的底等於(5^2-h^2)^1/2，一邊三角形的底等於(4^2-h^2)^1/2，而我們又知道兩個圓心的距離為8，也就是(5^2-h^2)^1/2+(4^2-h^2)^1/2=8。
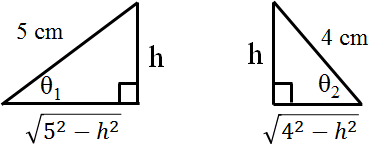
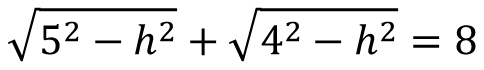
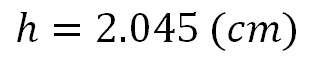
這邊可能會問，h是怎麼解出來的阿？
可以使用工程計算機或Excel求解，也可以點選以下WolframAplha網站求未知數。
WolframAplha求未知數 (點此進入頁面)
求得h之後，利用正弦定理求出θ1與θ2。
Sinθ1=(h/5)=(2.045/5)，θ1=24.142°
Sinθ2=(h/4)=(2.045/4)，θ2=30.747°
大的扇形面積(綠色扇形)=大圓半徑*大圓半徑*π*θ1/360=5*5*π*24.142/360=5.267 (cm^2)
小的扇形面積(藍色扇形)=小圓半徑*小圓半徑*π*θ2/360=4*4*π*30.747/360=4.293 (cm^2)
兩個大的扇形面積(綠色扇形)+兩個小的扇形面積(藍色扇形)=5.267*2+4.293*2=19.12 (cm^2)
菱形面積=兩對角線相乘積的一半=8*(2.045*2)/2=16.36 (cm^2)
重疊面積=兩個大的扇形面積(綠色扇形)+兩個小的扇形面積(藍色扇形)-菱形面積=19.12-16.36=2.76 (cm^2)
書籍分享
真希望國中數學這樣教：暢銷20萬冊！
奠定數學領域基礎！從1開始的數學啟蒙書：虛數‧證明
相對論，愛因斯坦教會我們什麼？
